Binary Indexed Tree (BIT) - An Introduction
Problem Statement
Imagine you are managing the scores of students in a classroom. You need to efficiently update a student's score and quickly calculate the total score over a range of students. Formally , there are N students in a classroom and the following two operations that can be performed:
- Update upd(i, val): Change points of student i to val.
- Sum sum(L, R): Sum the points of students from L to R [L..R].
Naïve Solution
(I) We can maintain an array A[1…N], where A[i] represents the points of the ith student. The operations can be performed as follows:
- Updating points of student i: A[i] = val
- Sum of points from L to R:
int sumR = 0 , sumL = 0 ;
for(int idx = 1 ; idx <= R ; ++idx)
sumR += A[idx] ; // sumR = sum[1…R]
for(int idx = 1 ; idx < L ; ++idx)
sumL += A[idx] ; // sumL = sum[1…L)
int ans = sumR + sumL /// sum = sum[L…R]
Here, the Update query runs in O(1) time, and the Sum query runs in O(N) time.
Optimizing with Prefix Sums
(II) By maintaining a prefix sum array, where p[i] stores the sum of the segment [1,i] (inclusive), the Sum query can be performed in O(1):
p[R] – p[L-1]
However, for an Update upd(i), we will need to change p[j] for all j ≥ i:
void update(int i, int val) {
int val_at_i = p[i] - p[i-1] ;//Value at index i
int delta = val - val_at_i ; // Change in value
for(int j = i ; j <= N ; ++j) {
p[i] += delta ; //Apply change
}
}
This approach handles the Sum query in O(1) but the Update query in O(N).
Takeaways
In each of these approaches, we are maintaining intervals and performing operations on them:
- For each index i, we maintain an interval that ends at that index. Each interval can be represented as [i, i] (in I) or [1, i] (in II).
- Update: When updating a student's points, we must update all intervals that include i. This involves updating the prefix sums or direct array elements.
- Sum: To find the sum between two indices, we calculate the difference between the prefix sums at R and L-1, or we manually sum the points in the naïve approach.
Simply put:
- S(R) = p[R] is the sum of the first R elements.
- Sum(L, R) = p[R] – p[L-1] gives the sum from L to R.
- The Binary Indexed Tree (BIT) offers a balanced approach to efficiently handle both update and sum operations.
Binary Indexed Tree (BIT)
To find a middle ground between the above two approaches, we use a Binary Indexed Tree (BIT), also known as a Fenwick Tree, to handle both Update and Sum operations efficiently.
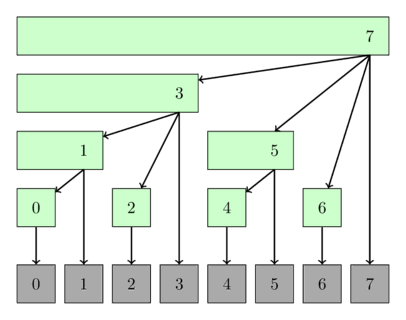
An element in BIT takes responsibility for a range rather than just itself.What do we mean by this responsibility and how do we decide the range for an element for which it will take responsibility ? In a BIT, each element doesn't just represent a single value; it represents the sum of values in a specific range. Consider the following array A (1-based indexing) :
LSB ((6)10) = (0110)2 = 0010 = 2 .
Thus an index i ending at 6 will take responsibility for 2 elements , given by the interval [6-2+1,6] = [5,6] .
In general, for any index i, the range of elements it covers is [i-b+1,i],where b is the value of the LSB of i.
- Indices where the LSB is 1 (e.g., 1, 3, 5, 7) take responsibility for just themselves.
- Indices where the LSB is 2 (e.g., 2, 6) take responsibility for 2 elements.
- Indices where the LSB is 4 (e.g., 4, 12) take responsibility for 4 elements, and so on.
So our BIT for the array A would look something like this :
Thus the index 6 stores the sum for 2 elements in [5,6] = 1 + 2 = 3
Similarly index 12 (LSB = 4) stores the sum for 4 elements in [9,12] = 2 + 1 + 4 + 3 = 10
Great ! So far we have now understood how a BIT works and stores the array . Now lets come back to our original problem of efficiently performing Update and sum query .
Sum(int pos) :
Consider we want the sum from indices [1,11] of array A. Now we start at index 11 and work our way down until no bits are left in our index.
sum = 0
Add the value at the current index to the sum:
sum += BIT[11] // LSB(11) = 1, responsible for [11, 11]
The least significant bit (LSB) of 11 is 1, which means that BIT[11] is responsible for the sum of the interval [11, 11].
Move to the next index by removing the LSB:
Subtract the LSB from the current index:
sum += BIT[10] // LSB(10) = 2, responsible for [9, 10]
After removing the LSB from 10, we move to index 8.
Repeat until no bits are left:
sum += BIT[8] // LSB(8) = 8, responsible for [1, 8]
Finally, BIT[8] is responsible for the interval [1, 8]. Since the LSB of 8 is 8, and subtracting it results in 0, we've now covered all relevant bits.
In this way we were able to calculate sum for [1,11]
Note : To calculate the sum over an arbitrary interval [L, R], use:
sum(L, R) = sum(R) - sum(L - 1)
Where sum(R) gives the sum of elements from 1 to R.
We can observe that in worst case , we might need to traverse all the bits , and the number of bits in a number is given by log2 N .
Hence our sum runs in O(log2 N) .
Update(int pos , int delta) :
In the update operation, we work our way upwards, modifying all the intervals that include the pos . Consider upd(5,10) where we want to add 10 to index 5 of our original array A.
In our BIT , all the indices which took responsibility of pos 5 will also add delta to themselves.
BIT[5] += delta // LSB(5) = 1, responsible for [5, 5]
The least significant bit (LSB) of 5 is 1, so BIT[5] is responsible for the interval [5, 5].
Move to the next index that includes 5:
pos = 5 + LSB(5) = 6
BIT[6] += delta // LSB(6) = 2, responsible for [5, 6]
The LSB of 6 is 2, so BIT[6] is responsible for the interval [5, 6].
Continue to the next relevant intervals:
pos = 6 + LSB(6) = 8
BIT[8] += delta // LSB(8) = 8, responsible for [1, 8]
Pos = 8 + LSB(8) = 16
BIT[8] += delta // LSB(16) = 16, responsible for [1, 16]
Finally, BIT[8] is updated since it is responsible for the interval [1, 8].
Just like the sum operation, the update operation also runs in O(log2 N) time, as in the worst case, we might need to update all bits in the index.
How to get the LSB ?
Since we now have a clear idea of how the update and sum operations take place in a Fenwick Tree and how we are able to get our answers for sum query , one thing that still remains unclear is how to get the Least significant set bit of a number . It can however be easily calculated by performing an AND operation b/w a number and its 2’s complement (~x + 1 or simply -x)
Thus LSB(x) = x & -x
Putting it all together
vector<int> bit(N+1,0) ; //N elements in 1-based indexing
//sum for [1,pos]
int query(int pos) {
int ans = 0 ;
while(pos > 0) { //While any bit is left in pos
ans += bit[pos] ; //add contribution of current pos to ans
pos -= (pos & -pos) ; //removing the lsb from pos
}
return ans ;
}
int querysum(int L , int R) {
return query(R) - query(L-1) ;
}
void update(int pos, int delta) {
while (pos <= N) { // While the position is within bounds
bit[pos] += delta; // Add delta to the BIT at position pos
pos += (pos & -pos); // Move to the next interval that includes pos
}
}
That’s it ,that was our small implementation for our complex data structure !
Our solution to the original problem would now look something like this :
void solve(){
int N ; //Number of studentes
cin >> N ;
vector<int> students(N+1,0) ; //1-nased indexing
for(int i = 1 ; i <= N ; ++i) cin >> students[i] ;
int M ; //number of queries
cin >> M ;
while(M--){
int type ;
cin >> type ; //Type of query
if(type == 1) {
//update query
int idx , val ;
cin >> idx >> val ;
// Compute the difference
int current_value = sum(idx) - sum(idx - 1); // Get current value at index
int delta = val - current_value; // Calculate the difference
// Update the BIT
update(idx, delta);
} else {
//sum query [L,R]
int L , R ;
cin >> L >> R ;
cout << querysum(R,L) << '\n';
}
}
}
The runtime of the solution has been improved from our naïve O(M*N) to O(M log2 N)
Count Inversions
Consider the following problem : Given an integer array A , return the number of inversions in the array .
An inversion is defined as a pair (i,j) where i < j and A[i] > A[j]
Example:
-
Input: A = [3, 1, 2]
-
Output: 2
Explanation: The inversions are (0, 1) and (0, 2).
Constraints : 1 <= N <= 105 , 1 <= A[i] <= 105
Approach : The idea is to iterate over the array in reverse order and for each element, count how many elements to its right are smaller than it.Our BIT keeps track of the frequencies of the element encountered so far . The number of elements smaller than our current element will simply be the sum of frequencies of elements less than our current element that can be retrieved using query(A[i]-1) and add this to our total inversions. (Note : Since we are considering only the smaller elements , we query(A[i]-1) and not A[i]) . After this we simply update our BIT to include our current element , and move on to the next element. A simple implementation would look like :
int countInversions(vector<int>& A) {
int N = A.size() ;
vector<int> bit(N + 1, 0); // Initialize BIT
int inversions = 0;
//Iterate from right to left
for (int i = N - 1; i >= 0; --i) {
// Count how many elements are smaller than A[i]
inversions += query(A[i] - 1);
// Update the BIT to include A[i]
update(A[i],1);
}
return inversions ;
}
Extension
The idea of Fenwick Tree presented in this blog is for Point Update and Range Query , However it can be easily modified to perform Range Update and Point Query or We can even maintain 2 BITs simultaneously to even perform Range Update and Range Query ! However there exists an even powerful Data Strucutre ( Segment Tree ) that can perform these tasks. The main idea benefit of using Fenwick Tree is the lesser lines of code it takes to code it up in an environment (let’s say an Interview) compared to a longer and complex code of Segment Tree
Fenwick Tree can also be extended to Multidimensional Arrays. A 2D Fenwick Tree can be used to perform update and query operations in a 2D Array .
Feel free to study about these extensions on your favourite Search engine !
Problems
Inversions (you might be required to first register in the pilot course)
Count of Smaller Numbers After Self
Count Good Triplets in an Array
References
CSA Academy : https://csacademy.com/lesson/fenwick_trees
TopCoder Tutroial : https://www.topcoder.com/thrive/articles/Binary%20Indexed%20Trees